Сила упругости

Отличия пружин подвески и их маркировка

Основным идентификационным параметром любой пружины служит ее наружный диаметр. Производители не могут его самопроизвольно изменить, так как этот размер определяется конструктивными особенностями самого автомобиля. Все остальные параметры могут быть абсолютно различными. Так производители могут:

1. изменить диаметр прута, из которого она изготавливается и даже использовать прут, имеющий диаметр переменного значения;
2. изготавливать пружины одинаковой высоты, но различной жесткости;
3. изменить межвитковое расстояние и количество витков, сохраняя при этом жесткость.

Статья в тему: Как зарегистрироваться на экзамен в ГИБДД через госуслуги? Поэтому на заводах перед установкой проводят контроль статистической нагрузки. Проводится такая операция следующим образом: измеряют высоту пружины, сжав ее с определенным усилием. Так как для каждой конкретной модели автомобиля высота в сжатом состоянии регламентирована полем допуска, то детали, не попавшие в это поле, выбраковываются.

Пружины, попавшие в границы верхнего поля допуска относят к классу А (длинные), а в категорию В (короткие) попадают те, что имеют высоту в пределах нижнего поля допуска. Далее пружины одного класса маркируют краской, причем цвет маркировки зависит от модели автомобиля, на котором они должны быть установлены.

• Пружины класса А автомобилей ВАЗ маркируют по цвету желтой, белой, коричневой и оранжевой красками.
• Вид В также маркируют по цвету, но зеленой, голубой, синей и черной красками.

Маркировка по цвету наносится на внешнюю сторону витков в виде цветной полоски. Обилие цветов маркировочной краски объясняется тем, что с целью уменьшения влияния коррозии, они подвергают специальному покрытию (хлоркаучуковая эмаль или защитное эпоксидное покрытие), которое также бывает разного цвета (черное, серое, синее, белое, голубое) и определяет как модель автомобиля, так и назначение пружины (передняя или задняя). Причем на заводах, выпускающих различные модели ВАЗ и «Лада», передние элементы окрашены, как правило, в черный цвет. Исключение составляют только пружины с переменным межвитковым расстоянием (шагом) — они окрашиваются в голубой цвет.

Статья в тему: Самостоятельное приготовление электролита для АКБ

Типы пружин

Пружины можно классифицировать по направлению прилагаемой нагрузки:

• пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны «виток к витку»; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
• пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.

В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип — запасать энергию упругой деформации и возвращать ее.

Готовые работы на аналогичную тему

• Курсовая работа Жесткость пружины, формула 490 руб.
• Реферат Жесткость пружины, формула 230 руб.
• Контрольная работа Жесткость пружины, формула 230 руб.

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

Количество пружин в матрасе — как выбрать

Для начала, надо разобраться над понятием независимых

. Абсолютно любая пружина находится в своем отдельном кармашке. Эти карманы связаны друг с другом лентами, а они приклеены. При тяжести на них, поджимается исключительно она, а остальные просто нет.

Главным преимуществом является то, что эти пружины оказывают колоссальное воздействие на позвоночник. Это говорит о том, что матрас будет достоверно передавать все очертания и изгибы вашего тела, учитывая такие показатели как рост и вес. Это достоинство будет работать не только когда будете лежать, но и, когда вы будете просто сидеть. Посмотрите на следующее фото:

Человек, который имеет больший вес будет изменять всю конструкцию, создавая как-бы яму, в которую будет съезжать ребенок с небольшим весом. Поэтому, если вы располагаете средствами, предпочтительнее остановить свой выбор на независимых конструкциях.

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями «цилиндров», диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние «цилиндры» при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

• $R$ — радиус цилиндра пружины,
• $n$ — количество витков проволоки радиуса $r$,
• $G$ — коэффициент, зависящий от материала.

Рассчитать коэффициент жесткости пружины, выполненной из стальной проволоки с $G = 8 cdot 10^<10>$ Па и диаметром 1 мм. Радиус пружины 20 мм, количество витков – 25.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

Ответ: $100 frac<Н><м>$

Так и не нашли ответ на свой вопрос?

Просто напиши с чем тебе нужна помощь

Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.

Жесткость пружины. Как рассчитать.

Измерение параметров жесткости пружин разных типов

При производстве на предприятии и для применения необходимо определить способность пружины выдерживать определенные типы нагрузок. Для этого высчитывается т.н. коэффициент Гука – обозначение жесткости пружины, от которого зависит её надёжность. На этот параметр влияет материал, выбранный для изготовления. Это может быть сталь, легированная кремнием, ванадием, марганцем, другими добавками. Также применяются нержавейка, бериллиевая и кремнемарганцевая бронза, сплавы на основе никеля и титана.

Если деталь выпускается для применения при высоких нагрузках, экстремальных температурах, используются специальные марки легированной стали. Нижегородская метизная корпорация имеет возможность производить пружины под заказ, создавая изделия с заданными характеристиками.

Что такое жесткость?

Говоря о практике, а не физических терминах, это сила, приложив которую, можно сжать пружину. Если вы знаете прилагаемое усилие, можно определить, какой будет деформация, и наоборот. Это существенно облегчает вычисления.

Коэффициент высчитывается для пружин кручения, растяжения, изгиба, сжатия – всех наиболее популярных в промышленности разновидностей этого изделия. Также следует отметить два основных типа:

• С линейной (постоянной) жесткостью;
• С прогрессивной (зависящей от положения витков) жесткостью.

Часто производитель наносит на готовую продукцию пометку краской. Если такого обозначения нет, применяется формула определения жесткости пружины через массу и длину, упрощающая задачу. Она изначально разрабатывалась для пружин растяжения, была получена методом измерения соответствия массы грузы с изменениями геометрии.

Также данный параметр может быть прогрессирующим – растущим — или регрессирующим – убывающим. Во втором случае параметр «жесткости» принято называть «мягкостью». В отдельных механизмах, например, в автомобилестроении, этот параметр особенно актуален.

Какие вводные данные требуются?

При расчёте важно знать следующую информацию:

• Из какого материала выполнено изделие;
• Точный диаметр витков – Dw;
• Общий диаметр самой пружины – Dm;
• Количество витков – Na.

Таким образом, к коэффициенту жесткости пружинного механизма может применяться формула:

Переменная G означает модуль сдвига. Это значение можно найти в таблицах для разных материалов. К примеру, у пружинной стали G=78,5 ГПа.

Далее разберемся, как определить жесткость пружины по формуле:

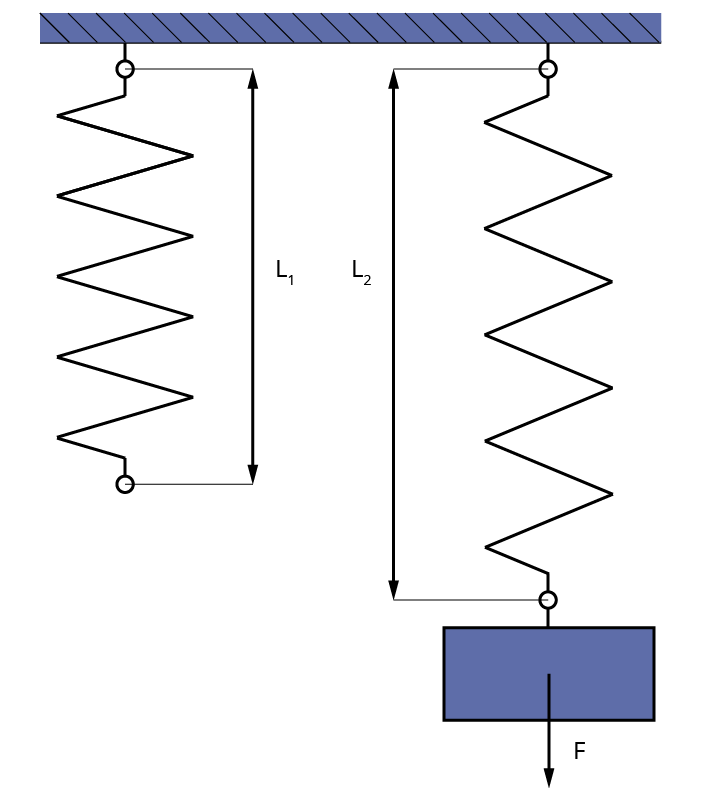
Длина L бывает двух типов:

• L1 – измеренная в вертикальном положении без груза;
• L2 – полученная при подвешивании груза с точно известной массой.

Например, 100-граммовая гиря, закреплённая в нижней части, воздействует с силой F, равной 1 Н. Получаем разницу между двумя показателями длины:

При этом следует уточнить, что степень жесткости не определяет распрямление в исходное состояние. На него воздействуют сразу несколько факторов.

Насколько важен показатель, и на что он влияет?

Характеристики пружины важны не только для соответствия ГОСТам и проведения сертификации. Они влияют на сроки эксплуатации изделий, в которых используются, а это огромное количество приборов, деталей, механизмов, от мебели, до различных транспортных средств.

Поэтому данная величина напрямую влияет на надёжность готовых изделий, оборудования, техники, в которых используются элементы, содержащие пружины.

Часто люди интересуются, как рассчитать жесткость пружины цилиндрической винтовой. Для таких случаев учитывается не только модуль сдвига, но и параметр Rs – напряжение, допускаемое при кручении. Здесь в расчёт берётся тип материала, его физические свойства, механические характеристики.

Следующий вопрос – в чем измеряется коэффициент жесткости пружины при расчётах. Традиционно в системе измерений, принятой в нашей стране принято записывать значение в Н/м – ньютонах на один метр. Также это значение в качестве альтернативного варианта может записываться в килограммах на квадратный сантиметр, дин/см, граммах на квадратный сантиметр (расчёты в системе СГС).

Зачем требуется маркировка цветом

Цветная маркировка, упрощающая жизнь автолюбителям при выборе, является следствием сложного процесса производства. Он характеризуется огромным количеством сложных технологических операций, которые очень трудно, а зачастую и невозможно, проконтролировать.

Поэтому все производители, осуществляющие массовый выпуск пружин, после изготовления считают необходимым проводить сравнительные анализы продукции. В результате этого появилась классификация по цвету, поскольку только так можно отличить разные по жесткости элементы после изготовления. Конечно, существуют и другие способы определить пружины разных видов, но этот самый простой и надежный.

Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765

Пружина сжатия                                                                                                                           Пружина растяжения

Наименование параметра	Обозначение	Расчетные формулы и значения
Сила пружины при предварительной деформации, Н	F 1	Принимается в зависимости от нагрузки пружины
Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н	F 3	Принимается в зависимости от нагрузки пружины
Рабочий ход пружины, мм	h	Принимается в зависимости от нагрузки пружины
Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с	v max	Принимается в зависимости от нагрузки пружины
Выносливость пружины, число циклов до разрушения	N F	Принимается в зависимости от нагрузки пружины
Наружный диаметр пружины, мм	D 1	Предварительно принимаются с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766…ГОСТ 13776
Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации	δ	δ = 1 — F 2 / F 3 (1) Для пружин сжатия классов I и II δ = 0,05 — 0,25 для пружин растяжения δ = 0,05 — 0,10 для одножильных пружин класса III δ = 0,10 — 0,40 для трехжильных класса III δ = 0,15 — 0,40
Сила пружины при максимальной деформации, Н	F 3	Уточняется по таблицам ГОСТ 13766 ÷ ГОСТ 13776
Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н	F	(0,1 ÷ 0,25) F 3
Диаметр проволоки, мм	d	Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776
Диаметр трехжильного троса, мм	d 1	Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776
Жесткость одного витка пружины, Н/мм	c 1	Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776
Максимальная деформация одного витка пружины, мм	s’ (при F = 0) s» (при F > 0)	Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776
Максимальное касательное напряжение пружины, МПа	τ 3	Для трехжильных пружин
Критическая скорость пружины сжатия, м/с	v k	Для трехжильных пружин
Модуль сдвига, МПа	G	Для пружинной сталиG = 7,85 х 104
Динамическая (гравитационная) плотность материала, Н • с2/м4	ρ	ρ = γ / g, где g — ускорение свободного падения, м/с2 γ — удельный вес, Н/м3 Для пружинной стали ρ = 8•103
Жесткость пружины, Н/мм	с	Для пружин с предварительным напряжением Для трехжильных пружин
Число рабочих витков пружины	n
Полное число витков пружины	n 1	где n2 — число опорных витков
Средний диаметр пружины, мм	D	Для трехжильных пружин
Индекс пружины	i	Для трехжильных пружин Рекомендуется назначать от 4 до 12
Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки	Δ	Для трехжильного троса с углом свивки β = 24° определяется по таблице i 4,0 4,5 5,0 5,5 6,0 7,0 и более Δ 1,029 1,021 1,015 1,010 1,005 1,000
Предварительная деформация пружины, мм	s 1
Рабочая деформация пружины, мм	s 2
Максимальная деформация пружины, мм	s 3
Длина пружины при максимальной деформации, мм	l 3	где n3 — число обработанных витков Для трехжильных пружин Для пружин растяжения с зацепами
Длина пружины в свободном состоянии, мм	l
Длина пружины растяжения без зацепов в свободном состоянии, мм	l’
Длина пружины при предварительной деформации, мм	l 1	Для пружин растяжения
Длина пружины при рабочей деформации, мм	l 2	Для пружин растяжения
Шаг пружины в свободном состоянии, мм	t	Для трехжильных пружин Для пружин растяжения
Напряжение в пружине при предварительной деформации, МПа	τ 1
Напряжение в пружине при рабочей деформации, МПа	τ 2
Коэффициент, учитывающий кривизну витка пружины	k	Для трехжильных пружин
Длина развернутой пружины (для пружин растяжения без зацепов), мм	l
Масса пружины (для пружин растяжения без зацепов), кг	m
Объем, занимаемый пружиной (без учета зацепов пружины), мм 3	V
Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм	λ	Устанавливается в зависимости от формы опорного витка
Внутренний диаметр пружины, мм	D 2
Временное сопротивление проволоки при растяжении, МПа	R m	Устанавливается при испытаниях проволоки или по ГОСТ 9389  и ГОСТ 1071
Максимальная энергия, накапливаемая пружиной, или работа деформации, мДж		Для пружин сжатия и растяжения без предварительного напряжения Для пружин растяжения с предварительным напряжением

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал \( F_{\text{упр}} \) силой упругости.

\

Эту формулу назвали законом упругости Гука.

\( F_{\text{упр}} \left( H \right) \) – сила упругости;

\( \Delta L \left(\text{м} \right) \)  – удлинение пружины;

\( \displaystyle k \left(\frac{H}{\text{м}} \right) \)  – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

\

Подставим в это уравнение выражение для силы упругости

\

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины \(\Delta L \) пружины. Получим выражение для коэффициента жесткости:

\

\(g\) – ускорение свободного падения, оно связано с силой тяжести.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l , где l — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Различные окраски маркировки пружин

Маркировка пружин также может быть и других окрасок и устанавливается в основном на заднюю подвеску машин-универсалов. Ранее – ВАЗ-2102, а сейчас – это ВАЗ-2104 и ВАЗ-2111. Маркировка пружин может быть различной длины и должна соответствовать характеристикам автомобиля. Возможно, ли монтировать данные пружины на седаны либо хэтчбеки? Для того, чтобы это выяснить необходимо определить цель монтирования подобных пружин на ваше авто. Если вы желаете повысить дорожный просвет вследствие проседания кузова, то эта установка для вас, поскольку она не скажется на ходовых особенностях машины. Но если вы хотите повысить процент нагрузки автомобиля более нормы, то лучше не применять данную операцию, поскольку возможно разрушение кузова и его износ раньше времени. В данном случае только автолюбитель может решить что лучше и важнее для него самого: выжать все «соки» из автомобиля за короткий срок либо сохранить его на долгое время.

Как использовать пружины соответственно их классу

Оба класса – «А» и «В», имеют абсолютно рабочие характеристики, и могут устанавливаться на автомобиль в равной степени. Единственное, что следует помнить при установке – цвета пружин подвески должны быть идентичны по обе стороны автомобиля. В противном случае может образоваться небольшой, но постоянный крен кузова на одну из сторон, что существенно ухудшит управляемость автомобилем и его устойчивость на дороге. Кроме того, если цвет пружин по жесткости будет отличаться, это приведет к ускоренному износу узлов всей «ходовки».

Специалисты достаточно часто говорят о необходимости использования на одном ТС элементов только одного класса. В крайнем случае, допускается устанавливать на переднюю ось пружины класса «А», на заднюю «В». Но ни в коем случае не наоборот – это категорически недопустимо. Чтобы избежать путаницы при самостоятельной замене, маркировка по цветам должна совпадать, так же как и их класс.

Формула определения жесткости

Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или

равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).

Другой вариант записи формулы: коэффициент Юнга

Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.

Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.

К примеру, модуль Юнга для ста

ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).

Смысл понятия коэффициент жесткости

Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.

Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).

Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:

• Материала, используемого при ее изготовлении.
• Формы и конструктивных особенностей.
• Геометрических размеров.

По этому показателю можно сд

елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.

Особенности расчета пружин

Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.

Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.

• Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
• При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.

Жесткость пружины. Как рассчитать.

Измерение параметров жесткости пружин разных типов

При производстве на предприятии и для применения необходимо определить способность пружины выдерживать определенные типы нагрузок. Для этого высчитывается т.н. коэффициент Гука – обозначение жесткости пружины, от которого зависит её надёжность. На этот параметр влияет материал, выбранный для изготовления. Это может быть сталь, легированная кремнием, ванадием, марганцем, другими добавками. Также применяются нержавейка, бериллиевая и кремнемарганцевая бронза, сплавы на основе никеля и титана. Если деталь выпускается для применения при высоких нагрузках, экстремальных температурах, используются специальные марки легированной стали. Нижегородская метизная корпорация имеет возможность производить пружины под заказ, создавая изделия с заданными характеристиками.

Что такое жесткость?

Говоря о практике, а не физических терминах, это сила, приложив которую, можно сжать пружину. Если вы знаете прилагаемое усилие, можно определить, какой будет деформация, и наоборот. Это существенно облегчает вычисления.

Коэффициент высчитывается для пружин кручения, растяжения, изгиба, сжатия – всех наиболее популярных в промышленности разновидностей этого изделия. Также следует отметить два основных типа:

• С линейной (постоянной) жесткостью;
• С прогрессивной (зависящей от положения витков) жесткостью.

Часто производитель наносит на готовую продукцию пометку краской. Если такого обозначения нет, применяется формула определения жесткости пружины через массу и длину, упрощающая задачу. Она изначально разрабатывалась для пружин растяжения, была получена методом измерения соответствия массы грузы с изменениями геометрии.

Также данный параметр может быть прогрессирующим – растущим — или регрессирующим – убывающим. Во втором случае параметр «жесткости» принято называть «мягкостью». В отдельных механизмах, например, в автомобилестроении, этот параметр особенно актуален.

Какие вводные данные требуются?

При расчёте важно знать следующую информацию:

• Из какого материала выполнено изделие;
• Точный диаметр витков – Dw ;
• Общий диаметр самой пружины – Dm ;
• Количество витков – Na .

Таким образом, к коэффициенту жесткости пружинного механизма может применяться формула:

k=G*(Dw)^4/8 * Na * (Dm)^3

Переменная G

означает модуль сдвига. Это значение можно найти в таблицах для разных материалов. К примеру, у пружинной сталиG=78,5 ГПа .

Далее разберемся, как определить жесткость пружины по формуле:

k=F/L.

Длина L

бывает двух типов:

• L1 – измеренная в вертикальном положении без груза;
• L2 – полученная при подвешивании груза с точно известной массой.

Например, 100

-граммовая гиря, закреплённая в нижней части, воздействует с силойF , равной1 Н . Получаем разницу между двумя показателями длины:

L = L2 – L1

При этом следует уточнить, что степень жесткости не определяет распрямление в исходное состояние. На него воздействуют сразу несколько факторов.

Насколько важен показатель, и на что он влияет?

Характеристики пружины важны не только для соответствия ГОСТам и проведения сертификации. Они влияют на сроки эксплуатации изделий, в которых используются, а это огромное количество приборов, деталей, механизмов, от мебели, до различных транспортных средств.

Поэтому данная величина напрямую влияет на надёжность готовых изделий, оборудования, техники, в которых используются элементы, содержащие пружины.

Часто люди интересуются, как рассчитать жесткость пружины цилиндрической винтовой. Для таких случаев учитывается не только модуль сдвига, но и параметр Rs

– напряжение, допускаемое при кручении. Здесь в расчёт берётся тип материала, его физические свойства, механические характеристики.

Следующий вопрос – в чем измеряется коэффициент жесткости пружины при расчётах. Традиционно в системе измерений, принятой в нашей стране принято записывать значение в Н/м

– ньютонах на один метр. Также это значение в качестве альтернативного варианта может записываться в килограммах на квадратный сантиметр, дин/см, граммах на квадратный сантиметр (расчёты в системе СГС).

Вопрос 8.4 Замена системы пружин эквивалентной пружиной

П

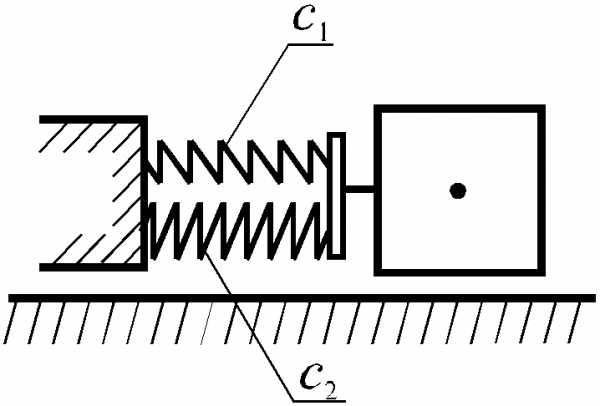
1 Параллельное соединение(рисунок 8.1).

П

Рисунок 8.1

2 Последовательное соединение(рисунок 8.2).

П

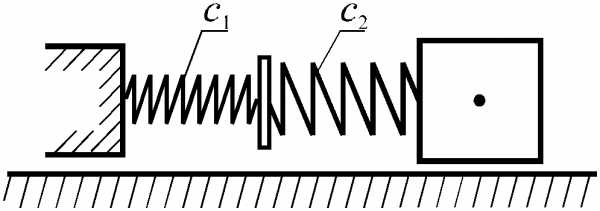
3

Рисунок 8.2

«Двухстороннее» соединение

П

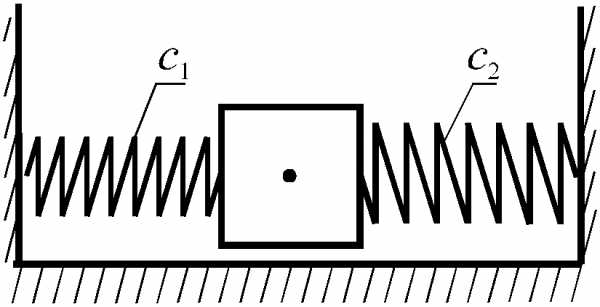
Любую систему пружин можно представить как набор рассмотренных схем.

Рисунок 8.3

Лекция 9 Динамика материальной системы.

(2 часа, 1 семестр, 2 курс)

Вопрос 9.1Теорема о движении центра масс материальной системы.

Центром масс материальной системы называют точку, радиус-вектор

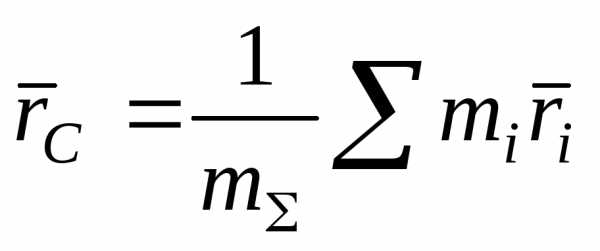
где

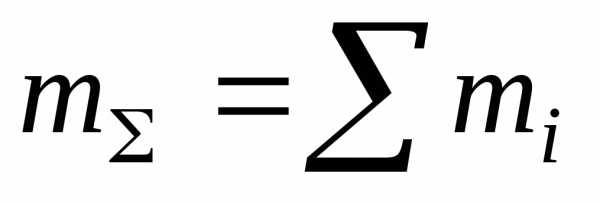
m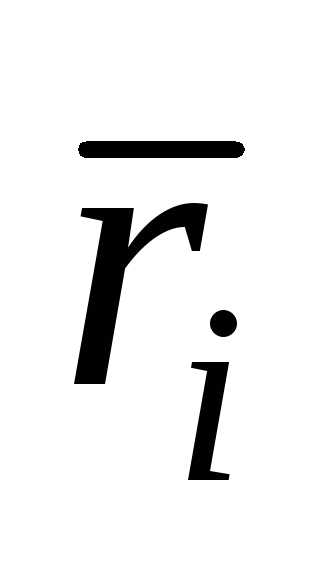_i,

i

,

где x_i,y_i,z_i– координаты центра массi-го тела системы.

При решении задач динамики материальной системы часто оказывается полезной теорема о движении центра масс:произведение массы материальной системы 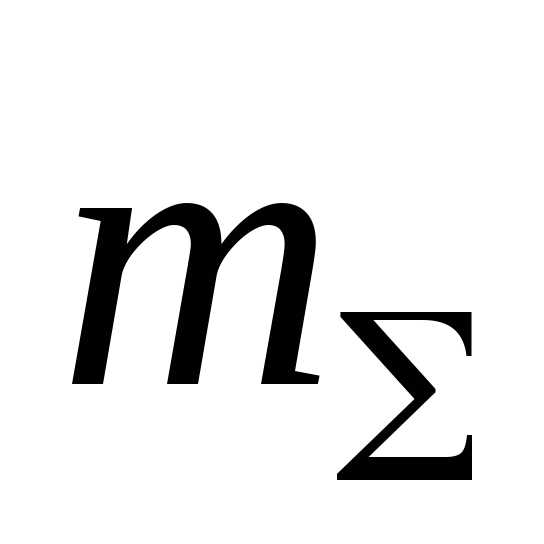на ускорение ее центра массa_C равно геометрической сумме внешних сил, приложенных к системе:

В ходе решения выражение теоремы проецируют на оси координат. При этом получается система уравнений

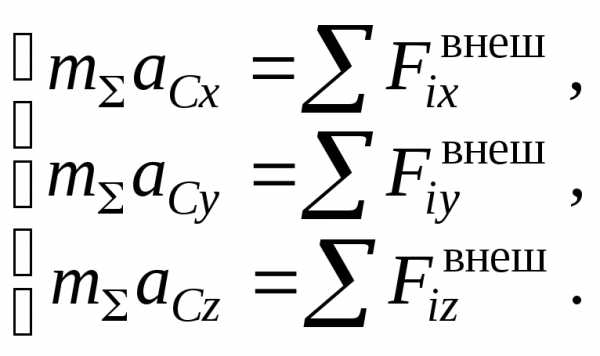
Использование теоремы о движении центра масс материальной системы для решения задач динамики рекомендуется осуществлять по следующей методике:

1 Изображается материальная система, и указываются все внешние силы, действующие на нее.

2 Выбираются оси координат.

3 Внешние силы, действующие на систему, проецируются на выбранные оси.

4 Записываются выражения координат центра масс системы через координаты центров масс одного из тел системы.

5 Дифференцируя выражения координат центра масс по времени, получают зависимости для скорости и ускорения центра масс системы.

6 Полученные выражения подставляются в систему динамических уравнений.

7 Решается дифференциальное уравнение относительно искомой координаты с учетом заданных начальных условий.

Вопрос 9.2Динамические уравнения движения твердого тела.

Динамические уравнения движения твердого тела устанавливают связь между кинематическими характеристиками движения тела и действующими на него силами.

Поступательное движение тела.В этом случае динамическое уравнение представляет собой следствие из теоремы о движении центра масс:

,

где m– масса тела;

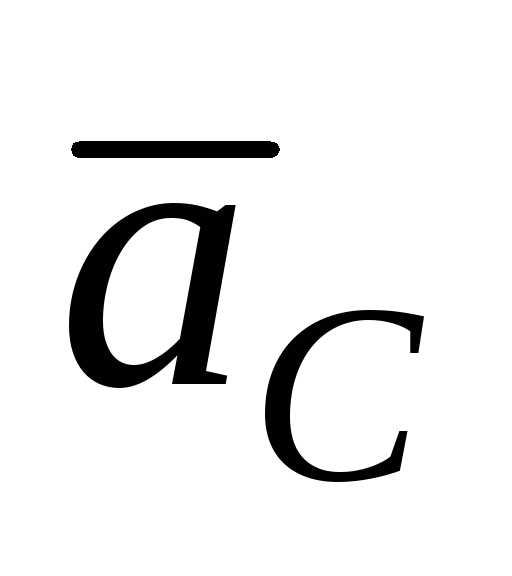
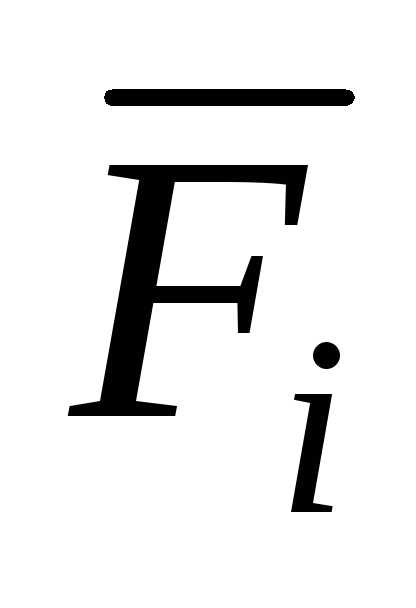i

При решении задач динамическое уравнение поступательного движения тела проецируют на оси координат.

Вращательное движение тела. Для него динамическое уравнение имеет вид:

,

где J_z– момент инерции тела относительно оси вращенияz;

 – угловое ускорение тела;

M_iz– моментi-й силы относительно оси вращения.

При составлении динамического уравнения вращательного движения тела выбирается направление отсчета угла поворота . Моменты сил, вращающих тело против выбранного направления, принимаются отрицательными, а по выбранному направлению – положительными.

Момент инерции J_z является мерой инертности тела при вращательном движении. Момент инерции материальной системы относительно данной осиOzопределяется как сумма произведений масс всех точек системы на квадраты их расстояний от этой оси:

Для абсолютно твердого тела суммирование по точкам системы заменяется интегрированием по объему

,

где ρ – плотность материала тела;

h– расстояние от точки с координатамиx,y,zдо осиOz.

Момент инерции J_Cтела относительно осиCz, проходящей через центр массC, называютцентральным моментом инерции. Если для тела известенрадиус инерцииi, то центральный момент

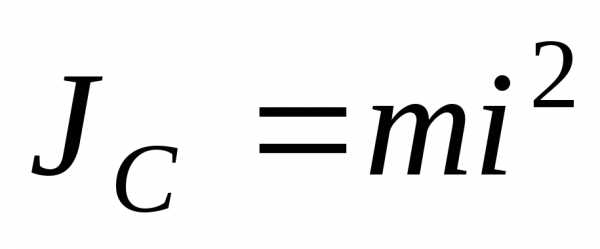
Центральные моменты инерции некоторых тел:

1 Тонкий однородный стержень с массой mи длинойl:

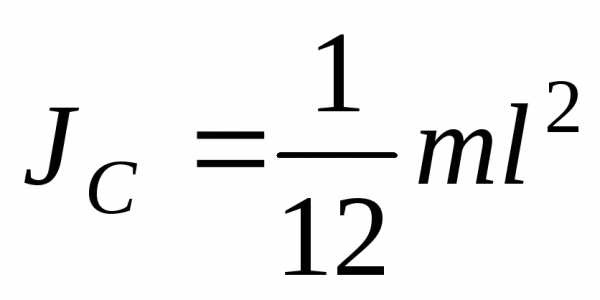
2 Тонкое круглое однородное кольцо с массой mи радиусомR:

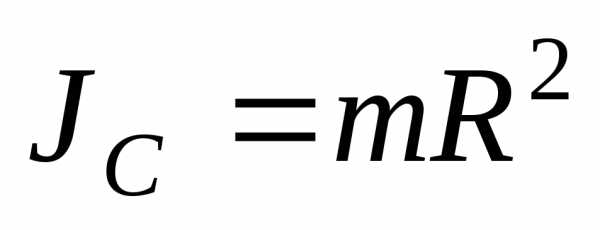
3 Круглый однородный диск с массой mи радиусомR: