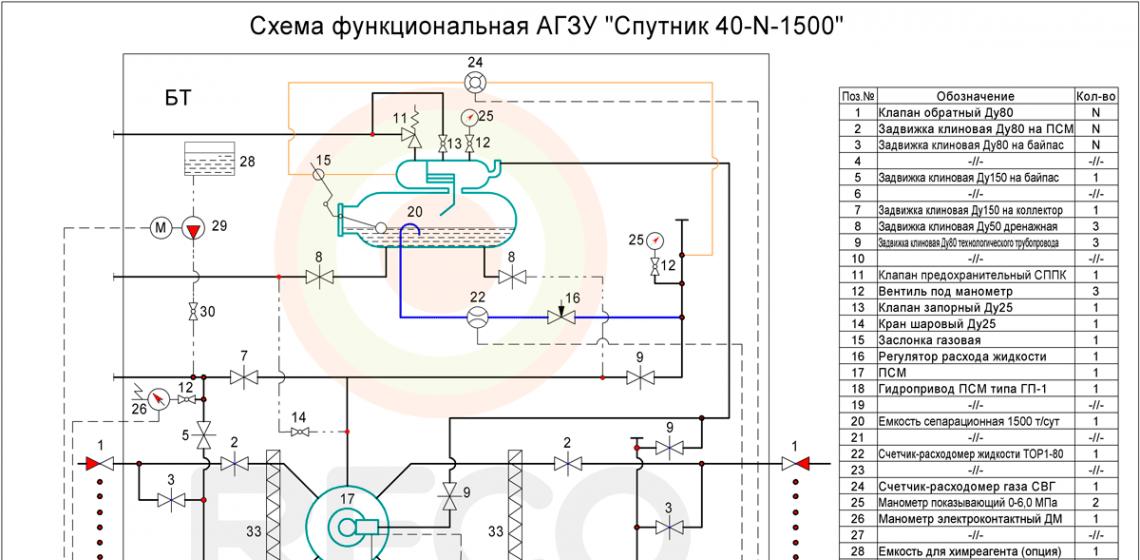
Расчет максимальной скорости автомобиля. расчет кпп
Содержание:
- Калькулятор КПП и главной пары
- Расчет третей передачи редуктора
- 5. Расчет передачи заднего хода редуктора (шестерня – шестерня паразитная)
- Мощности
- Крутящий момент редуктора
- Передаточное число [I]
- Как рассчитать передаточное число
- Калькулятор передаточных чисел кпп
- Передаточное отношение зубчатой передачи
- Назначение, конструктивные особенности
- Классификация по числу ступеней и типу передачи
- Калькулятор передаточных чисел кпп
- Онлайн расчеты :: SS20 Sport Club
- Выбираем тип редуктора
- Передаточное число [I]
- Общее определение
- Онлайн расчеты :: SS20 Sport Club
- 5 . 1 Проектировочный расчет
- Исходные данные:
Калькулятор КПП и главной пары
| R колеса | |
| Ширина колеса | |
| Профиль | |
| Обороты двигателя | 500100015002000250030003500400045005000550060006500700075008000850090009500100001050011000 |
| Главная пара | 3.9 3.5 3.74.14.34.54.74.95.16.8 |
| 1-я передача | 3.63 (станд.) 2.92 (5-й ряд)2.92 (6-й ряд) 2.92 (7-й ряд)3.42 (8-й ряд) 3.42 (10-й ряд)3.63 (11-й ряд) 3.16 (12-й ряд) 3.17 (15-й ряд)3.17 (18-й ряд) 3.17 (20-й ряд)3.17 (102-й ряд)2.92 (103-й ряд)2.92 (104-й ряд)2.92 (200-й ряд)3.0 (026-й ряд) 3.0 (711-й ряд) 2.67 (745-й ряд)2.67 (74-й ряд) |
| 2-я передача | 1.95 (станд.)1.81 (5-й ряд)1.81 (6-й ряд)2.05 (7-й ряд)2.05 (8-й ряд)2.05 (10-й ряд)2.22 (11-й ряд)1.95 (12-й ряд)1.81 (15-й ряд)2.11 (18-й ряд)1.9 (20-й ряд)1.95 (102-й ряд)1.95 (103-й ряд)1.95 (104-й ряд)2.22 (200-й ряд)2.53 (026-й ряд) 2.53 (711-й ряд) 1.93 (745-й ряд)1.93 (74-й ряд) |
| 3-я передача | 1.36 (станд.)1.28 (5-й ряд)1.28 (6-й ряд)1.56 (7-й ряд)1.36 (8-й ряд)1.36 (10-й ряд)1.54 (11-й ряд)1.36 (12-й ряд)1.28 (15-й ряд)1.48 (18-й ряд)1.26 (20-й ряд)1.36 (102-й ряд)1.36 (103-й ряд)1.36 (104-й ряд)1.76 (200-й ряд)2.06 (026-й ряд) 2.06 (711-й ряд) 1.59 (745-й ряд)1.56 (74-й ряд) |
| 4-я передача | 0.94 (станд.)0.97 (5-й ряд)1.06 (6-й ряд)1.31 (7-й ряд)0.97 (8-й ряд)0.97 (10-й ряд)1.17 (11-й ряд)1.03 (12-й ряд)0.94 (15-й ряд)1.13 (18-й ряд)0.94 (20-й ряд)0.94 (102-й ряд)0.94 (103-й ряд)1.03 (104-й ряд)1.39 (200-й ряд)1.74 (026-й ряд) 1.74 (711-й ряд) 1.37 (745-й ряд)1.37 (74-й ряд) |
| 5-я передача | 0.78 (станд.)0.78 (5-й ряд)0.94 (6-й ряд)1.13 (7-й ряд)0.78 (8-й ряд)0.78 (10-й ряд)0.89 (11-й ряд)0.78 (12-й ряд)0.73 (15-й ряд)0.89 (18-й ряд)0.73 (20-й ряд)0.73 (102-й ряд)0.69 (103-й ряд)0.73 (104-й ряд)1.17 (200-й ряд)1.48 (026-й ряд) 1.48 (711-й ряд) 1.2 (745-й ряд)0.79 (74-й ряд) |
| 6-я передача | нет0.69 (станд.)0.94 (7-й ряд)0.78 (18-й ряд)0.94 (200-й ряд) |
| Результаты: | |
martaler.ru
Расчет третей передачи редуктора
3.1
Проектировочный расчет
Исходные данные:
Количество зубьев шестерни: ;
Количество зубьев колеса: ;
Требуемое передаточное отношение: ;
Частота вращения шестерни: ;
КПД подшипников качения :;
КПД передачи: ;
Срок службы: .
|
Элемент передачи |
Марка стали | Термообработка | Заготовка | Твердость поверхности | ||
| Шестерня | 40ХН | Объемная закалка | поковка | 1600 | 1400 | 56HRCэ |
| Колесо | 40ХН | Объемная закалка | поковка | 1600 | 1400 | 55HRCэ |
Определение частот вращения и угловых скоростей валов:
— ведущего:
;
— ведомого:
.
Базовое число циклов перемены напряжений шестерни и колеса:
Определение чисел циклов перемены напряжений шестерни и колеса:
;
;
.
Определение допускаемых напряжений:
а) контактные
:
;
где:;
;
;
;
;
В качестве расчетного принимаем .
б) изгибные
:
,
где:;
, т.к. ;
;
.
в) предельные
:
8.Определение коэффициентов расчетной нагрузки:
При твердости , 8-ой степени точности и
;
Принимаем ;
9.Определим начальный (делительный) диаметр шестерни:
где:,
X=0.0061(100-Z)
X1=0.5063, X2=0.4331
=0.02976981,
, ,
,
Из конструктивных соображений .
10.Модуль зацепления:
По ГОСТ 9563-60 , тогда
3.2 Проверочный расчет
1.Проверка передачи на контактную выносливость:
Предварительно устанавливаем следующие параметры:
для прямозубых колес.
Окружная скорость:
Коэффициент расчетной нагрузки:
Принимаем:
Определяем удельную расчетную окружную силу:
Недогрузка равна 1.6%.
2.Проверка передачи на изгибную выносливость:
;
, для ;
, для ;
; .
3.Проверка на контактную и изгибную прочность при действии максимальной нагрузки (проверка на перегрузку, на предотвращение пластической деформации или хрупкого излома):
Определение геометрических размеров шестерни и колеса:
4. Проверочный расчет четвертой передачи редуктора
Исходные данные:
Количество зубьев шестерни: ;
Количество зубьев колеса: ;
Требуемое передаточное отношение: ;
Частота вращения шестерни: ;
КПД подшипников качения :;
КПД передачи: ;
Срок службы: .
1.Проверка передачи на контактную выносливость:
X=0.0061(100-Z)
X1=0.4758, X2=0.4638
=0.2977,
, ,
,
Окружная скорость:
Коэффициент расчетной нагрузки:
Принимаем:
Определяем удельную расчетную окружную силу:
Недогрузка равна 0,4%.
2.Проверка передачи на изгибную выносливость:
;
, для ;
, для ;
; .
3.Проверка на контактную и изгибную прочность при действии максимальной нагрузки (проверка на перегрузку, на предотвращение пластической деформации или хрупкого излома):
,
;
6. Определение геометрических размеров шестерни и колеса:
5. Расчет передачи заднего хода редуктора
(шестерня – шестерня паразитная)
Мощности
При вращательных движениях рабочих органов механизмов возникает сопротивление, которое приводит к трению – истиранию узлов. При грамотном выборе редуктора по показателю мощности он способен преодолевать это сопротивление. Потому этот момент имеет большое значение, когда нужно купить мотор-редуктор с долгосрочными целями.
Сама мощность – Р – считается как частное от силы и скорости редуктора. Формула выглядит так:
- где:M – момент силы;
- N – обороты в минуту.
Для выбора нужного мотор-редуктора необходимо сопоставить данные по мощности на входе и выходе – Р1 и Р2 соответственно. Расчет мощности мотор-редуктора на выходе рассчитывается так:
где:P – мощность редуктора;Sf – эксплуатационный коэффициент, он же сервис-фактор.
На выходе мощность редуктора (P1 > P2) должна быть ниже, чем на входе. Норма данного неравенства объясняется неизбежными потерями производительности при зацеплении в результате трения деталей между собой.
При расчете мощностей обязательно применять точные данные: из-за разных показателей КПД вероятность ошибки выбора при использовании приблизительных данных близится к 80%.
Крутящий момент редуктора
Крутящий момент на выходном валу – вращающий момент на выходном валу. Учитывается номинальная мощность , коэффициент безопасности , расчетная продолжительность эксплуатации (10 тысяч часов), КПД редуктора.
Номинальный крутящий момент – максимальный крутящий момент, обеспечивающий безопасную передачу. Его значение рассчитывается с учетом коэффициента безопасности – 1 и продолжительность эксплуатации – 10 тысяч часов.
Максимальный вращающий момент – предельный крутящий момент, выдерживаемый редуктором при постоянной или изменяющейся нагрузках, эксплуатации с частыми пусками/остановками. Данное значение можно трактовать как моментальную пиковую нагрузку в режиме работы оборудования.
Необходимый крутящий момент – крутящий момент, удовлетворяющим критериям заказчика. Его значение меньшее или равное номинальному крутящему моменту.
Расчетный крутящий момент – значение, необходимое для выбора редуктора. Расчетное значение вычисляется по следующей формуле:
Mc2 = Mr2 x Sf ≤ Mn2
где Mr2 – необходимый крутящий момент; Sf – сервис-фактор (эксплуатационный коэффициент); Mn2 – номинальный крутящий момент.
Передаточное число [I]
Передаточное число редуктора рассчитывается по формуле:
I = N1/N2
где N1 – скорость вращения вала (количество об/мин) на входе; N2 – скорость вращения вала (количество об/мин) на выходе.
Полученное при расчетах значение округляется до значения, указанного в технических характеристиках конкретного типа редукторов.
Таблица 2. Диапазон передаточных чисел для разных типов редукторов
| Тип редуктора | Передаточные числа |
| Червячный одноступенчатый | 8-80 |
| Червячный двухступенчатый | 25-10000 |
| Цилиндрический одноступенчатый | 2-6,3 |
| Цилиндрический двухступенчатый | 8-50 |
| Цилиндрический трехступенчатый | 31,5-200 |
| Коническо-цилиндрический одноступенчатый | 6,3-28 |
| Коническо-цилиндрический двухступенчатый | 28-180 |
ВАЖНО! Скорость вращения вала электродвигателя и, соответственно, входного вала редуктора не может превышать 1500 об/мин. Правило действует для любых типов редукторов, кроме цилиндрических соосных со скоростью вращения до 3000 об/мин
Этот технический параметр производители указывают в сводных характеристиках электрических двигателей.
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
u12 = ± Z2/Z1 и u21 = ± Z1/Z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.
Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
u16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.
КПД зубчатой передачи
Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:
- трение соприкасаемых поверхностей;
- изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
- потери на шпонках и шлицах;
- трение в подшипниках.
Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.
При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.
Калькулятор передаточных чисел кпп
Расчет передаточных чисел трансмиссии начинают с расчета передаточного числа на первой и высшей передачах. Номер высшей передачи зависит от того, сколько ступеней предполагается у коробки передач проектируемого автомобиля (три, четыре, пять. ). Передаточное число первой передачи должно обеспечивать преодоление наибольшего дорожного сопротивления движению автомобиля. В этом случае значения касательного усилия, исходя из подведенного крутящего момента двигателя при Мkmax, желательно иметь равным максимальному касательному усилию по сцеплению, т.е.
, (10)
где iтр1,тр1— соответственно передаточное число и КПД на первой передаче;
к— коэффициент нагрузки ведущих колес; для 4х2к = 0,70. 0,75; для 4х4к = 1,0;
rк— динамический радиус ведущих колес, м;
Ма— полная масса автомобиля;
g- ускорение свободного падения;
— максимальное значение коэффициента сцепления (принимается в пределах 0,7. 0,8).
Рис. 1. Внешняя скоростная характеристика карбюраторного двигателя
Передаточное отношение зубчатой передачи
Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.
При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.
Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.
Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.
Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.
Передаточное отношение редуктора вычисляется по формуле:
где U12 – передаточное отношение шестерни относительно колеса;
ω1 и ω2 – угловые скорости ведущего и ведомого элемента соединения;


Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Назначение, конструктивные особенности
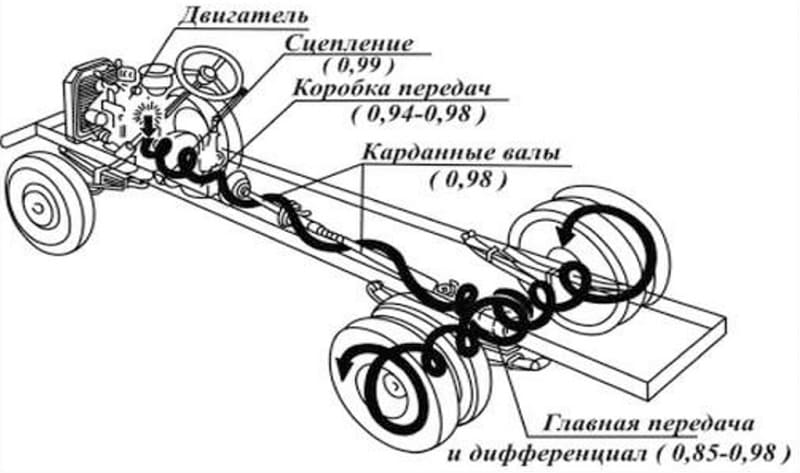
Основная задача этого элемента сводится к изменению крутящего момента перед подачей его на привод колес. То же делает и коробка передач, но у неё существует возможность изменения передаточных чисел за счет ввода в зацепление тех или иных шестерен. Несмотря на наличие в конструкции автомобиля КПП, на выходе из нее крутящий момент небольшой, а скорость вращения выходного вала – высокая. Если передать вращение напрямую на ведущие колеса, то возникшая нагрузка «задавит» двигатель. В общем, авто просто не сможет сдвинуться с места.
Главная передача автомобиля обеспечивает повышение крутящего момента и снижение скорости вращения. Но в отличие от КПП передаточное число у нее фиксированное.
Расположение главной передачи на примере обычной МКПП
Представляет собой эта передача на легковом авто обычный шестеренчатый одноступенчатый редуктор постоянного зацепления, состоящий из двух шестерен разного диаметра. Ведущая шестерня небольшая по размерам и связана она с выходным валом КПП, то есть вращение подается на нее. Ведомая же шестерня значительно больше по размерам и получаемое вращение она подает на приводные валы колес.
Передаточное число является соотношением количества зубьев шестерен редуктора. Для легковых авто этот параметр находится в диапазоне 3,5-4,5, а для грузовиков он достигает 5-7.
Чем больше передаточное число (больше количество зубьев ведомой шестерни относительно ведущей), тем выше крутящий момент, подаваемый на колеса. При этом тяговое усилие будет больше, но максимальная скорость ниже.
Передаточное число главное передачи подбирается исходя из эксплуатационных показателей силовой установки, а также других узлов трансмиссии.
Устройство главной передачи напрямую зависит от конструктивных особенностей самого автомобиля. Этот редуктор может быть, как отдельным узлом, установленным в своем картере (заднеприводные модели), так и входить в конструкцию КПП (авто с передним приводом).
Главная передача в заднеприводном автомобиле
Что касается некоторых полноприводных авто, то у них может использоваться разная компоновка. Если в таком автомобиле расположение силовой установки – поперечное, то главная передача передней оси входит в конструкцию КПП, а задней располагается в отдельном картере. У автомобиля с продольной компоновкой главные передачи на обоих осях отделены от КПП и раздаточной коробки.
В моделях с отделенной главной передачей, этот редуктор выполняет еще одну задачу – изменяет угол направления вращения на 90 град. То есть выходной вал КПП и приводные валы колес имеют перпендикулярное расположение.
Расположение главной передачи передней оси Audi
В переднеприводных моделях, где главная передача входит в конструкцию КПП, указанные валы имеют параллельное расположение, поскольку менять угол направления не нужно.
В ряде грузовых авто применяются двухступенчатые редукторы. Примечательно, что их конструкция может быть разной, но наибольшее распространение получила так называемая разнесенная компоновка, в которой используется один центральный редуктор и два колесных (бортовых). Такая конструкция позволяет существенно повысить крутящий момент, а соответственно и тяговое усилие на колесах.
Привод легковых автомобилей
Особенность работы редуктора сводится к тому, что он равномерно разделяет вращение на оба приводных вала. При прямолинейном движении такое условие является нормальным. Но при прохождении поворотов колеса одной оси проходят разное расстояние, поэтому необходимо изменение скорости вращения каждого из них. Это входит в задачу дифференциала, используемого в конструкции трансмиссии (он устанавливается на ведомой шестерне). В результате главная передача подает вращение на приводные валы не напрямую, а через дифференциал.
Классификация по числу ступеней и типу передачи
| Тип редуктора | Число ступеней | Тип передачи | Расположение осей |
|---|---|---|---|
| Цилиндрический | 1 | Одна или несколькоцилиндрических | Параллельное |
| 2 | Параллельное/соосное | ||
| 3 | |||
| 4 | Параллельное | ||
| Конический | 1 | Коническая | Пересекающееся |
| Коническо-цилиндрический | 2 | КоническаяЦилиндрическая(одна или несколько) | Пересекающееся/Скрещивающееся |
| 3 | |||
| 4 | |||
| Червячный | 1 | Червячная(однаили две) | Скрещивающееся |
| 2 | Параллельное | ||
| Цилиндро-червячный или червячно- цилиндрический | 2 | Цилиндрическая (одна или две)Червячная (одна) | Скрещивающееся |
| 3 | |||
| Планетарный | 1 | Два центральныхзубчатых колеса и сателлиты (для каждой ступени) | Соосное |
| 2 | |||
| 3 | |||
| Цилиндрическо-планетарный | 2 | Цилиндрическая (одна или несколько) Планетарная (одна или несколько) | Параллельное/соосное |
| 3 | |||
| 4 | |||
| Коническо-планетарный | 2 | Коническая (одна) Планетарная (одна или несколько) | Пересекающееся |
| 3 | |||
| 4 | |||
| Червячно-планетарный | 2 | Червячная (одна) Планетарная (одна или несколько) | Скрещивающееся |
| 3 | |||
| 4 | |||
| Волновой | 1 | Волновая (одна) | Соосное |
Калькулятор передаточных чисел кпп
Расчет передаточных чисел трансмиссии начинают с расчета передаточного числа на первой и высшей передачах. Номер высшей передачи зависит от того, сколько ступеней предполагается у коробки передач проектируемого автомобиля (три, четыре, пять. ). Передаточное число первой передачи должно обеспечивать преодоление наибольшего дорожного сопротивления движению автомобиля. В этом случае значения касательного усилия, исходя из подведенного крутящего момента двигателя при Мkmax, желательно иметь равным максимальному касательному усилию по сцеплению, т.е.
, (10)
где iтр1,тр1— соответственно передаточное число и КПД на первой передаче;
к— коэффициент нагрузки ведущих колес; для 4х2к = 0,70. 0,75; для 4х4к = 1,0;
rк— динамический радиус ведущих колес, м;
Ма— полная масса автомобиля;
g- ускорение свободного падения;
— максимальное значение коэффициента сцепления (принимается в пределах 0,7. 0,8).
Рис. 1. Внешняя скоростная характеристика карбюраторного двигателя
Онлайн расчеты :: SS20 Sport Club
Исходные данные
Диаметр обода Ширина колеса Обороты двигателя Главная пара
3.53.73.94.14.34.54.74.95.1
Первая передача
2.92 (5-й ряд)2.92 (6-й ряд) 2.92 (7-й ряд)3.42 (8-й ряд)3.42 (10-й ряд)3.63 (станд.)3.63 (11-й ряд)3.16 (12-й ряд)3.17 (15-й ряд)3.17 (18-й ряд)3.17 (20-й ряд)3.17 (102-й ряд)2.92 (103-й ряд)2.92 (104-й ряд)2.92 (200-й ряд)3.0 (026-й ряд)3.0 (711-й ряд)2.67 (745-й ряд)2.67 (74-й ряд)
Вторая передача
1.81 (5-й ряд)1.81 (6-й ряд)2.05 (7-й ряд)2.05 (8-й ряд)2.05 (10-й ряд)2.22 (11-й ряд)1.95 (станд.)1.95 (12-й ряд)1.81 (15-й ряд)2.11 (18-й ряд)1.9 (20-й ряд)1.95 (102-й ряд)1.95 (103-й ряд)1.95 (104-й ряд)2.22 (200-й ряд)2.53 (026-й ряд) 2.53 (711-й ряд) 1.93 (745-й ряд)1.93 (74-й ряд)
Третья передача
1.28 (5-й ряд)1.28 (6-й ряд)1.56 (7-й ряд)1.36 (станд.)1.36 (8-й ряд)1.36 (10-й ряд)1.54 (11-й ряд)1.36 (12-й ряд)1.28 (15-й ряд)1.48 (18-й ряд)1.26 (20-й ряд)1.36 (102-й ряд)1.36 (103-й ряд)1.36 (104-й ряд)1.76 (200-й ряд)2.06 (026-й ряд)2.06 (711-й ряд)2.06 (45-й ряд)1.56 (74-й ряд)
Четвертая передача
0.94 (станд.)0.97 (5-й ряд)1.06 (6-й ряд)1.31 (7-й ряд)0.97 (8-й ряд)0.97 (10-й ряд)1.17 (11-й ряд)1.03 (12-й ряд)0.94 (15-й ряд)1.13 (18-й ряд)0.94 (20-й ряд)0.94 (102-й ряд)0.94 (103-й ряд)1.03 (104-й ряд)1.39 (200-й ряд)1.74 (026-й ряд)1.74 (711-й ряд)1.37 (745-й ряд)1.37 (74-й ряд)
Пятая передача
0.78 (станд.)0.78 (5-й ряд)0.94 (6-й ряд)1.13 (7-й ряд)0.78 (8-й ряд)0.78 (10-й ряд)0.89 (11-й ряд)0.78 (12-й ряд)0.73 (15-й ряд)0.89 (18-й ряд)0.73 (20-й ряд)0.73 (102-й ряд)0.69 (103-й ряд)0.73 (104-й ряд)1.17 (200-й ряд)1.48 (026-й ряд)1.48 (711-й ряд)1.2 (745-й ряд)0.79 (74-й ряд)
Шестая передача
нет0.69 (станд.)0.94 (7-й ряд)0.78 (18-й ряд)0.94 (200-й ряд)
Рассчитать
ss20club.ru
Выбираем тип редуктора
Для того, чтобы определиться с типом редуктора, нужно рассмотреть пространственное расположение всех механизмов, которые присоединяются к редуктору, их места креплений и способы монтажа.
- Цилиндрические редукторы:
- Горизонтальный тип такого редуктора подходит для схем, в которых оси входного и выходного валов между собой параллельны и при этом находятся в одной плоскости (а именно, горизонтальной);
- У вертикального цилиндрического типа оси редуктора должны располагаться в одной вертикальной плоскости;
- Планетарный или соосный цилиндрический тип используется в том случае, если оси валов находятся в разных плоскостях, но при этом расположены на одной прямой.
- Коническо-цилиндрические редукторы применяются только для тех схем, где оси валов находятся в одной плоскости (горизонтальной) и перпендикулярны друг другу.
- Червячные редукторы:
- Оси одноступенчатого червячного редуктора должны скрещиваться под прямым углом и лежать в разных плоскостях;
- У двухступенчатого червячного редуктора оси валов пересекаются под прямым углом или параллельны друг другу, но при этом обязательно лежат в разных плоскостях.
Более того, в зависимости от области применения редуктора могут оказать влияние такие факторы, как:
- Громкость работы (самый «тихий» — червячный редуктор);
- КПД или коэффициент полезного действия (самые эффективные в плане работы считаются планетарные редукторы, в то время как у двухступенчатых червячных редукторов КПД самый низкий);
- Стоимость в относительном эквиваленте (планетарные редукторы считаются самыми недорогими).
Также, производя расчет червячного редуктора, следует учитывать тот факт, что его использование в большей мере оправдано при повторяющихся кратковременных режимах эксплуатации.
Передаточное число [I]
Передаточное число редуктора рассчитывается по формуле:
I = N1/N2
где N1 – скорость вращения вала (количество об/мин) на входе; N2 – скорость вращения вала (количество об/мин) на выходе.
Полученное при расчетах значение округляется до значения, указанного в технических характеристиках конкретного типа редукторов.
Таблица 2. Диапазон передаточных чисел для разных типов редукторов
| Тип редуктора | Передаточные числа |
| Червячный одноступенчатый | 8-80 |
| Червячный двухступенчатый | 25-10000 |
| Цилиндрический одноступенчатый | 2-6,3 |
| Цилиндрический двухступенчатый | 8-50 |
| Цилиндрический трехступенчатый | 31,5-200 |
| Коническо-цилиндрический одноступенчатый | 6,3-28 |
| Коническо-цилиндрический двухступенчатый | 28-180 |
ВАЖНО! Скорость вращения вала электродвигателя и, соответственно, входного вала редуктора не может превышать 1500 об/мин. Правило действует для любых типов редукторов, кроме цилиндрических соосных со скоростью вращения до 3000 об/мин
Этот технический параметр производители указывают в сводных характеристиках электрических двигателей.
Общее определение
Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.
Передачи с крутящим моментом
В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:
Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудовании для изменения скорости вращения рабочего узла, в автомобилях.
Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.
Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.
На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.
Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.
Характеристика зубчатой передачи
В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.
Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.
Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.

Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.
Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.
Зачем нужна паразитка
При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:
- количества оборотов;
- мощности;
- направление вращения.
Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.
Онлайн расчеты :: SS20 Sport Club
Исходные данные
Диаметр обода Ширина колеса Обороты двигателя Главная пара
3.53.73.94.14.34.54.74.95.1
Первая передача 2.92 (5-й ряд)2.92 (6-й ряд) 2.92 (7-й ряд)3.42 (8-й ряд)3.42 (10-й ряд)3.63 (станд.)3.63 (11-й ряд)3.16 (12-й ряд)3.17 (15-й ряд)3.17 (18-й ряд)3.17 (20-й ряд)3.17 (102-й ряд)2.92 (103-й ряд)2.92 (104-й ряд)2.92 (200-й ряд)3.0 (026-й ряд)3.0 (711-й ряд)2.67 (745-й ряд)2.67 (74-й ряд) Вторая передача
1.81 (5-й ряд)1.81 (6-й ряд)2.05 (7-й ряд)2.05 (8-й ряд)2.05 (10-й ряд)2.22 (11-й ряд)1.95 (станд.)1.95 (12-й ряд)1.81 (15-й ряд)2.11 (18-й ряд)1.9 (20-й ряд)1.95 (102-й ряд)1.95 (103-й ряд)1.95 (104-й ряд)2.22 (200-й ряд)2.53 (026-й ряд) 2.53 (711-й ряд) 1.93 (745-й ряд)1.93 (74-й ряд)
Третья передача
1.28 (5-й ряд)1.28 (6-й ряд)1.56 (7-й ряд)1.36 (станд.)1.36 (8-й ряд)1.36 (10-й ряд)1.54 (11-й ряд)1.36 (12-й ряд)1.28 (15-й ряд)1.48 (18-й ряд)1.26 (20-й ряд)1.36 (102-й ряд)1.36 (103-й ряд)1.36 (104-й ряд)1.76 (200-й ряд)2.06 (026-й ряд)2.06 (711-й ряд)2.06 (45-й ряд)1.56 (74-й ряд)
Четвертая передача 0.94 (станд.)0.97 (5-й ряд)1.06 (6-й ряд)1.31 (7-й ряд)0.97 (8-й ряд)0.97 (10-й ряд)1.17 (11-й ряд)1.03 (12-й ряд)0.94 (15-й ряд)1.13 (18-й ряд)0.94 (20-й ряд)0.94 (102-й ряд)0.94 (103-й ряд)1.03 (104-й ряд)1.39 (200-й ряд)1.74 (026-й ряд)1.74 (711-й ряд)1.37 (745-й ряд)1.37 (74-й ряд) Пятая передача
0.78 (станд.)0.78 (5-й ряд)0.94 (6-й ряд)1.13 (7-й ряд)0.78 (8-й ряд)0.78 (10-й ряд)0.89 (11-й ряд)0.78 (12-й ряд)0.73 (15-й ряд)0.89 (18-й ряд)0.73 (20-й ряд)0.73 (102-й ряд)0.69 (103-й ряд)0.73 (104-й ряд)1.17 (200-й ряд)1.48 (026-й ряд)1.48 (711-й ряд)1.2 (745-й ряд)0.79 (74-й ряд)
Шестая передача
нет0.69 (станд.)0.94 (7-й ряд)0.78 (18-й ряд)0.94 (200-й ряд)
Рассчитать
ss20club.ru
5 . 1 Проектировочный расчет
Исходные данные:
Количество зубьев шестерни: ;
Количество зубьев колеса: ;
Требуемое передаточное отношение: ;
Частота вращения шестерни: ;
КПД подшипников качения :;
КПД передачи: ;
Срок службы: .
Таблица 5.1
| Элемент передачи | Марка стали | Термообработка | Заготовка | Твердость поверхности | ||
| Шестерня | 20Х2Н4А | Цементация | поковка | 1400 | 1200 | 65HRCэ |
| Колесо | 20Х2Н4А | Цементация | поковка | 1400 | 1200 | 63HRCэ |
Определение числа циклов перемены напряжений шестерни и колеса:
, , ;
, , ,
Определение допускаемых напряжений:
а) контактных:
, ,
так как и , то, а , ,
для колеса -,
для шестерни — ,
,
в качестве расчётного принимаем ;
б) изгибные:
, так как , то , ,
,
;
в) предельные:
,
.
Определение коэффициентов расчётной нагрузки
Коэффициенты расчётной нагрузки соответственно при расчётах на контактную и изгибную выносливость равны:
,
kHa= kFa=1
,
.
Определение начального диаметра шестерни
,
где, ,
X=0.0061(100-Z)
X1=0.56, X2=0.51
=0.08678,
, ,
,
— коэффициент ширины шестерни относительно её диаметра,
.
Определение модуля зацепления
Принимаемm
=2.75мм ,тогда
,
Mежосевое расстояние: .
5.2 Проверочный расчёт
Проверка передачи на контактную прочность:
,
Zm=275 МПа1/2
Определим окружную скорость:
,
уточним коэффициент расчётной нагрузки:
,
,
следовательно: ,
,
определяем удельную расчётную окружную силу:
,
,
Недогруз составляет 0,7%. что допустимо.
Проверка зубьев передачи на изгибную выносливость
.
а) Определим коэффициенты формы зубьев шестерни и колеса:
для ,
для ,
, .
б) Проверяем на прочность зуб шестерни:
,
, где
.
Проверка на контактную и изгибную прочность при действии максимальной нагрузки (проверка на перегрузку, на предотвращение пластической деформации или хрупкого излома):
,
Конструирование зубчатого колеса и шестерни
Определение геометрических и других размеров шестерни и колеса
— диаметр вершин зубьев:
,
,
— диаметр впадин зубьев:
,
6. Расчет передачи заднего хода редуктора
(Шестерня паразитная — колесо)
6.1
Проектировочный расчет
Исходные данные:
Количество зубьев шестерни: ;
Количество зубьев колеса: ;
Требуемое передаточное отношение: ;
Частота вращения шестерни: ;
КПД подшипников качения :;
КПД передачи: ;
Срок службы: .
Таблица 6.1
| Элемент передачи | Марка стали | Термообработка | Заготовка | Твердость поверхности | ||
| Шестерня | 20Х2Н4А | Цементация | поковка | 1400 | 1200 | 65HRCэ |
| Колесо | 20Х2Н4А | Цементация | поковка | 1400 | 1200 | 63HRCэ |
Определение числа циклов перемены напряжений шестерни и колеса:
, , ;
, , ,
Определение допускаемых напряжений:
а) контактных:
,
,
так как и , то, а , ,
для колеса -,
для шестерни — ,
,
в качестве расчётного принимаем ;
б) изгибные:
, так как , то , ,
,
;
в) предельные:
,
.
Определение коэффициентов расчётной нагрузки
Коэффициенты расчётной нагрузки соответственно при расчётах на контактную и изгибную выносливость равны:
,
kHa= kFa=1
,
.
Определение начального диаметра шестерни
,
где, ,
X=0.0061(100-Z)
X1=0.51, X2=0.427
, ,
,
— коэффициент ширины шестерни относительно её диаметра,
.
Определение модуля зацепления
Принимаемm
=2.75мм ,тогда
,
Mежосевое расстояние: .
6.2
Проверочный расчёт
Проверка передачи на контактную прочность:
,
Zm=275 МПа1/2
Определим окружную скорость:
,
уточним коэффициент расчётной нагрузки:
,
,
следовательно: ,
,
определяем удельную расчётную окружную силу:
,
,
Проверка зубьев передачи на изгибную выносливость
.
а) Определим коэффициенты формы зубьев шестерни и колеса:
для ,
для ,
, .
б) Проверяем на прочность зуб шестерни:
,
, где
.
Проверка на контактную и изгибную прочность при действии максимальной нагрузки (проверка на перегрузку, на предотвращение пластической деформации или хрупкого излома):
,
Конструирование зубчатого колеса и шестерни
Определение геометрических и других размеров шестерни и колеса
— диаметр вершин зубьев:
,
,
— диаметр впадин зубьев:
,
7. Расчет валов
7.1 Расчет вала-шестерни